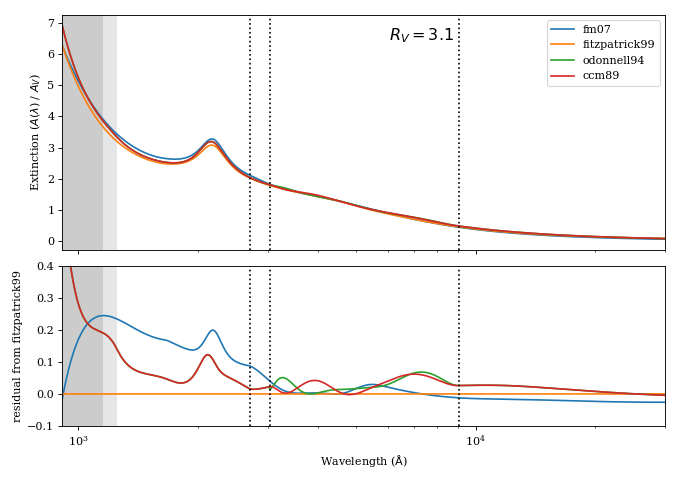
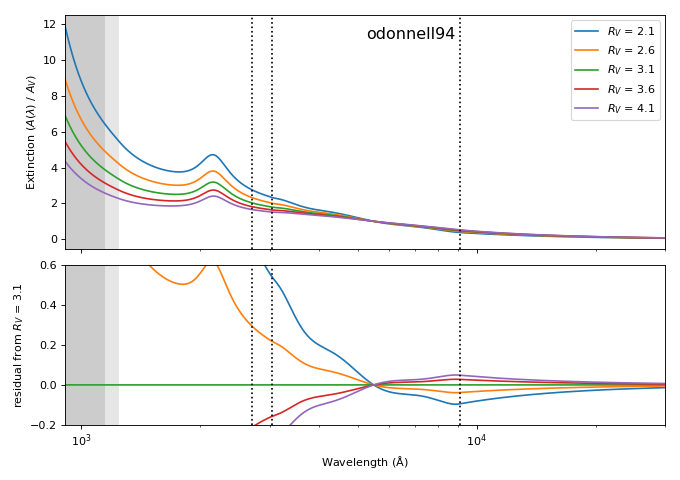
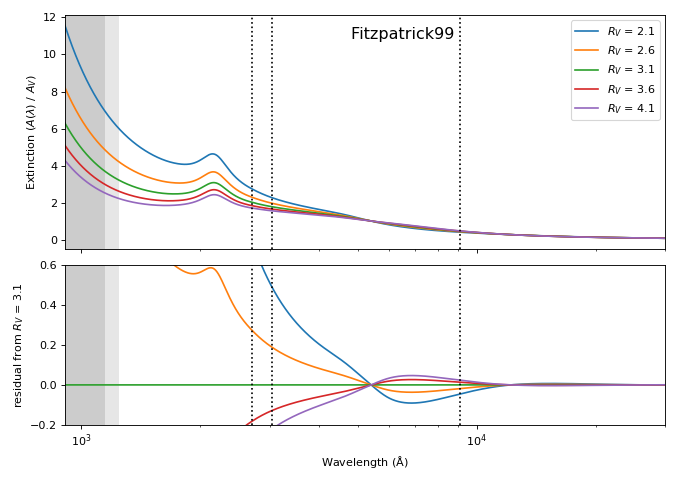
extinction¶
Fast interstellar dust extinction laws in Python
Cython-optimized implementations of empirical dust exitinction laws found in the literature.
Installation¶
Using conda:
conda install -c conda-forge extinction
Using pip (requires a C compiler):
pip install extinction
Extinction depends on numpy and scipy.
Development version / source code: http://github.com/kbarbary/extinction
Usage¶
Functions:
extinction.ccm89(wave, a_v, r_v[, unit, out]) |
Cardelli, Clayton & Mathis (1989) extinction function. |
extinction.odonnell94(wave, a_v, r_v[, …]) |
O’Donnell (1994) extinction function. |
extinction.calzetti00(wave, a_v, r_v[, …]) |
Calzetti (2000) extinction function. |
extinction.fitzpatrick99(wave, a_v[, r_v, unit]) |
Fitzpatrick (1999) dust extinction function. |
extinction.fm07(wave, a_v[, unit]) |
Fitzpatrick & Massa (2007) extinction model for R_V = 3.1. |
extinction.apply(extinction, flux[, inplace]) |
Apply extinction to flux values. |
extinction.remove(extinction, flux[, inplace]) |
Remove extinction from flux values. |
Classes:
extinction.Fitzpatrick99 |
Fitzpatrick (1999) dust extinction function for arbitrary R_V. |
Examples:
Get extinction in magnitudes at a set of wavelengths for various dust laws:
>>> import numpy as np
>>> import extinction
>>> wave = np.array([2000., 4000., 8000.]) # wavelength in Angstroms
# Cardelli, Clayton & Mathis (1989) with A_V = 1 and R_V = 3.1
>>> extinction.ccm89(wave, 1.0, 3.1)
array([ 2.84252644, 1.4645557 , 0.59748901]) # extinction in magnitudes
# O'Donnell (1994)
>>> extinction.odonnell94(wave, 1.0, 3.1)
array([ 2.84252644, 1.42617802, 0.60793495])
# Fitzpatrick (1999)
>>> extinction.fitzpatrick99(wave, 1.0, 3.1)
array([ 2.76225609, 1.79674653, 1.42325373])
The Fitzpatrick & Massa (2007) function has a fixed \(R_V\) of 3.1:
>>> extinction.fm07(wave, 1.0)
array([ 2.90478329, 1.42645161, 0.54703201])
All extinction laws accept a unit keyword to change the interpretation of
the wavelength array from Angstroms to inverse microns:
>>> wave = np.array([5., 2.5, 1.25]) # wavelength in inverse microns
>>> extinction.ccm89(wave, 1.0, 3.1, unit='invum')
array([ 2.84252644, 1.4645557 , 0.59748901]) # extinction in magnitudes
Redden or deredden¶
To “redden” or “deredden” flux values by some amount, use the
apply and remove convenience functions:
>>> from extinction import ccm89, apply
>>> flux = np.ones(3)
# "redden" flux by A_V = 1.0
>>> apply(ccm89(wave, 1.0, 3.1), flux)
array([ 0.07294397, 0.25952412, 0.5767723 ])
# "deredden" flux by A_V = 1.0
>>> remove(ccm89(wave, 1.0, 3.1), flux)
array([ 13.70915145, 3.85320647, 1.73378645])
A note on parameterization¶
Most extinction laws here have two parameters: \(A_V\) and
\(R_V\). \(A_V\) is a simply a linear scaling parameter; that
is: ccm89(wave, 2.0, 3.1) is the same as 2.0 * ccm89(wave, 1.0,
3.1). \(R_V\) changes the shape of the extinction
curve, rather than just the amplitude.
Traditionally, the meaning ascribed to these parameters was that \(A_V\) is the extinction in the V band, and \(R_V\) describes the ratio of total to selective extinction: \(R_V = A_V / E(B-V)\), where \(E(B-V)\) is the difference in extinction between the B and V bands. While this is approximately correct, the measured extinction of a source in actual B and V bandpasses will generally depend on the source spectrum and the shape of the specific bandpasses. Therefore, the \(A_V\) and \(R_V\) that are parameters in our extinction law will not correspond perfectly to measured B and V extinctions. So, in the context of these extinction laws, it is best to think of \(A_V\) and \(R_V\) as simply parameters that describe the amplitude and shape of the wavelength dependence, rather than corresponding directly to measured magnitudes.
Finally, for a given shape of the extinction curve (described by \(R_V\)), one can equally well use \(E(B-V)\) as a linear scaling parameter in place of \(A_V\), with the equivalence \(E(B-V) = A_V / R_V\). Note that the above caution applies here: \(E(B-V)\) should be considered simply a parameter describing amplitude of extinction; it will not correspond exactly to a difference in measured B and V extinctions.
License and Credits¶
The license is MIT. Part of this code originated in the specutils package.